نتحدث عن إضافة وطرح المتجهات من خلال هذه المقالة. ونذكر لكم أيضًا تاريخ المتجهات وإضافة المتجهات على الرسم البياني ومكونات المتجهات، ونختتم الموضوع بمفهوم الكميات المتجهة. تابع السطور التالية.
إضافة وطرح المتجهات
جمع المتجهات:
يمكن جمع المتجهات عن طريق إضافة مكونات المتجهات معًا؛ أي جمع المكونات السيني، وإضافة مكونات y، وجمع مكونات العينة بشكل منفصل، أو يمكن جمع المتجهات بطريقة هندسية؛ بحيث يتم وضع المتجه الأول، ثم يتم وضع ذيل المتجه الثاني فوق الأول، وهكذا، وفي النهاية يتم رسم سهم من ذيل المتجه الأول إلى رأس المتجه الأخير، و ونتيجة الجمع هي هذا المتجه الأخير الذي تم رسمه، والذي يعرف بالمتجه الناتج، ومجموع المتجهات يخضع للخاصيتين التبادلية والترابطية. لجمع.
خطة الاتجاهات:
عملية الطرح في المتجهات هي نفس عملية الجمع، ولكن بدلاً من إضافة متجهين، يتم إضافة المتجه الأول إلى سالب المتجه الثاني. أي إضافة المتجه الثاني بعد عكس اتجاهه.
تاريخ المتجهات
لقد مر مفهوم المتجهات بمراحل عديدة من التطور حتى نراه في شكله المعاصر. على مدار 200 عام، قدم العديد من العلماء العديد من المساهمات في تطوير مفهوم المتجهات. قام جوستو بيلافيتا بتلخيص وتوضيح الفكرة الرئيسية للأطروحة في عام 1935 عندما أسس مفهوم المتجهات. Equipollence”، وقدم العالم ويليام روان هاميلتون لاحقًا مصطلح المتجه، وقام العديد من العلماء، بقيادة هيرمان جراسمان، والكونت دي سينتس، وأوغسطين كوشي، وماثيو أوبراين، وأوغسطس موبيوس بتطوير العديد من أنظمة المتجهات المماثلة في منتصف القرن التاسع عشر. قرن.
في عام 1840، طور غروسمان نظرية الانجراف، وهي أول نظام تحليلي مكاني مشابه لنظام اليوم. في عام 1878، نشر ويليام كينغدون كليفورد كتاب “العناصر الديناميكية” وقام بتبسيط بعض الدراسات التي سبقته. نشر إدوين بيدويل ويلسون في عام 1901 تحليل المتجهات، والذي تم تعديله من محاضرات جيب، ونفى أي ذكر لمسألة التأخير في عملية تطوير المتجهات في حساب التفاضل والتكامل.
إضافة ناقلات على الرسم البياني
افترض أن متجهين يعملان على كائن ما. وباستخدام الرسم البياني يمكننا تحديد النتيجة، كما يلي:
1- نرسم المتجهين على شكل أسهم بمقياس محدد من حيث المقدار والاتجاه.
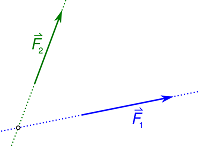
2- نرسم خطاً موازياً للسهم الثاني من طرف السهم الأول.
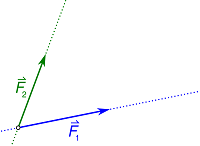
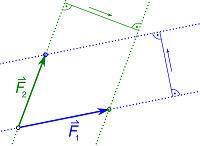
3- نرسم خطاً موازياً للسهم الأول من طرف السهم الثاني. يتقاطع الخطان ويكتمل متوازي الأضلاع.
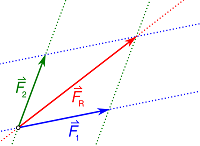
4- المحور الذي يبدأ من نقطة تأثير المتجهين إلى نقطة تقاطع الخطين هو محصلة المتجهين ومقامهما.
مكونات المتجهات
– لأي متجه هناك مكونات تعتمد على النظام الإحداثي الذي نحن فيه، وفي هذه المقالة سيتم الحديث عن نظام الإحداثيات الديكارتية. يمكن التعبير عن جميع المتجهات في المستوى الديكارتي من خلال المكونات السيني والسيني y والسيني، حيث أن أي متجه يساوي مجموع هذه المكونات الثلاثة، أي المكون السيني. مضروبًا في متجه الوحدة السيني، والمكون y مضروبًا في متجه الوحدة y، والمكون السيني مضروبًا في متجه الوحدة السيني، والمكون عبارة عن تعبير يتعلق بطول المتجه على طول محاور نظام الإحداثيات المستخدم، ويمكن القول أن طول المتجه على طول
كما ذكرنا سابقًا، يظهر متجه الوحدة عند التعبير عن المتجهات باستخدام المكونات. يمكن تعريف متجه الوحدة على أنه متجه بلا أبعاد له حجم واحد، ويعبر اتجاهه عن اتجاه كل مكون من مكونات المتجه. تختلف متجهات الوحدة حسب نظام الإحداثيات المستخدم، وإذا كان لدينا متجه في… المستويين x وy فقط، وإذا كانت الزاوية بين المحور x والمتجه هي (φ)، فإن مقدار سيكون مكون المحور x مساوياً لطول هذا المتجه مضروبًا في جيب تمام الزاوية (φ)، وسيكون طول المكون y مساويًا لطول المتجه مضروبًا في جيب الزاوية (φ) ).
مفهوم الكميات المتجهة
في الفيزياء، المتجه هو كمية لها مقدار واتجاه. ويمثل عادة بسهم اتجاهه هو نفس اتجاه الكمية ويتناسب طوله مع حجم الكمية. على الرغم من أن المتجه له مقدار واتجاه، إلا أنه ليس له موضع، أي ما دام طوله لا يتغير. ولا يتغير المتجه إذا تحرك موازيًا لنفسه.
– على عكس المتجهات، تسمى الكميات المنتظمة التي لها مقدار وليس اتجاه الكميات العددية. على سبيل المثال، الإزاحة والسرعة والتسارع هي كميات متجهة، في حين أن السرعة (كمية السرعة) والوقت والكتلة هي كميات قياسية.
– للتأهل كمتجه، يجب أيضًا أن تخضع الكمية التي لها مقدار واتجاه لقواعد معينة للجمع، إحدى هذه القواعد هي إضافة المتجهات، والتي تكتب رمزيًا بالشكل A + B = C (يتم كتابة المتجهات تقليديًا بأحرف غامقة)، وبشكل هندسي يمكن تصور مجموع المتجه من خلال وضع ذيل المتجه B على قمة المتجه A وارسم المتجه C بدءًا من ذيل A وينتهي عند قمة B – لإكمال المثلث.
-إذا كانت A وB وC متجهات، فمن الممكن إجراء نفس العملية وتحقيق نفس النتيجة (C) بترتيب عكسي، B + A = C. الكميات مثل الإزاحة والسرعة لها هذه الخاصية (القانون) التبادل)، ولكن هناك كميات (على سبيل المثال، الدوران المحدود في الفضاء) ليست متجهات، وبالتالي ليست متجهات.
القواعد الأخرى للتعامل مع المتجهات هي الطرح، والضرب بعدد قياسي، والضرب العددي (المعروف أيضًا باسم حاصل الضرب النقطي أو المنتج الداخلي)، وضرب المتجهات (المعروف أيضًا باسم المنتج المتقاطع)، والتمايز. لا توجد عملية تقابل القسمة على المتجه.