محصلة المتجهات في الفيزياء

المتجه الناتج في الفيزياء، والمقصود بتحليل المتجهات، وأنواع المتجهات، وخصائص المتجهات، هذا ما سنتعرف عليه فيما يلي.

المتجهات الناتجة في الفيزياء

عندما يتحرك جسم بين نقطتين أو أكثر، تتولد إزاحات متعددة لها قيمة واتجاه. ومن أجل إيجاد النتيجة النهائية للإزاحة الكلية للجسم بين النقطتين الأولى والأخيرة، يتم إضافة هذه الإزاحات إلى بعضها البعض أو طرح هذه الإزاحات من بعضها البعض (إذا كان اتجاهها متعاكساً). ولذلك فإن طريقة إيجاد المحصلة يمكن تقسيم الإزاحات إلى نوعين:

1- إضافة المتجهات:

عند إضافة متجهين أو أكثر لبعضهما البعض، يجب أن تكون هذه الكميات المتجهة من نفس النوع (الإزاحات أو القوى، على سبيل المثال) ويجب أن تكون وحدات قياس متطابقة.
2-طرح المتجهات:

تستخدم هذه الطريقة لإيجاد محصلة إزاحتين أو أكثر عندما تكونا متقابلتين في الاتجاه أو كليا. يمكن استخدام مفهوم المتجه السالب (سالب المتجه) لتغيير عملية طرح المتجهات إلى عملية جمع ومن ثم التعامل معها. يتم تعريف المتجه السالب على أنه متجه، إذا تمت إضافته إلى المتجه الأصلي، فسيؤدي إلى أن يكون مجموع المتجهين صفرًا. على سبيل المثال، إذا أضيف المتجه السالب (-A) إلى المتجه A، فإن مجموع محصلة المتجهين سيكون صفراً، حيث يكون المتجه -A مساوياً في القيمة للمتجه A وعكسه في الاتجاه، كما يلي:
أ+ (-أ) = 0
وبناء على هذا المفهوم يمكن تحويل عملية طرح أي متجهين إلى عملية جمع عن طريق أخذ المتجه السالب للثاني كما يلي:
أب = أ+(-ب)
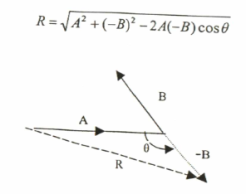
يمثل الشكل التالي عملية طرح متجهين، حيث يلاحظ أن المتجه B يعارض جزئيًا اتجاه حركة المتجه A. ويحدث هذا إذا تجاوزت الزاوية بين المتجهين المتتاليين 90 درجة. وبالتالي، يمكن رسم المتجه B في الاتجاه المعاكس للمتجه B، بشرط أن يكون مساويًا له في الحجم، حيث عندها فقط يمكن معاملة المتجه A والمتجه B كمجموع متجه. لإيجاد قيمة الحركة الناتجة R، يجب أن نعرف الزاوية θ بين المتجه A والمتجه B، ثم نستخدم قانون جيب التمام.

ميزة أخرى مهمة للمتجهات هي أنه إذا تم ضربها بكمية غير متجهة (عددية)، فإن النتيجة هي متجه جديد قيمته تساوي حاصل ضرب قيمة المتجه في قيمة الكمية القياسية، و سيكون اتجاهه في اتجاه رئيس الوزراء. وكمثال على ذلك، إذا تم ضرب المتجه A بالكمية غير المتجهة m، فإن النتيجة تساوي:
(mA = B = A×m)، حيث B هو المتجه الجديد.

ما هو تحليل المتجهات؟

هو فرع من فروع الرياضيات يتعامل مع الكميات من حيث الحجم والاتجاه. يمكن تحديد بعض الكميات الفيزيائية والهندسية، والتي تسمى الكميات، بشكل كامل عن طريق تحديد حجمها بوحدات القياس المناسبة. وبالتالي، يمكن التعبير عن الكتلة بالجرام، ودرجة الحرارة بالدرجات على المقياس، والوقت بالثواني. يمكن تمثيل القياسات بيانياً بنقاط على بعض المقاييس الرقمية مثل الساعة أو مقياس الحرارة. هناك أيضًا كميات، تسمى المتجهات، والتي تتطلب تحديد الاتجاه وكذلك الحجم. السرعة والقوة والإزاحة هي أمثلة على المتجهات. يمكن تمثيل الكمية المتجهة بيانياً بقطعة خطية موجهة، يرمز لها بسهم يشير في اتجاه كمية المتجهات، ويمثل طول القطعة مقدار المتجه.

أنواع المتجهات

1-النواقل الأولية المشتركة

تسمى المتجهات التي لها نفس نقطة البداية بالنواقل الأولية المشتركة.
2-المتجه الصفري

المتجه الصفري هو متجه عندما يكون مقدار المتجه صفرًا وتتزامن نقطة بداية المتجه مع النقطة النهائية، ويترتب على ذلك أن مقدار المتجه الصفري هو صفر واتجاه هذا المتجه غير محدد.
3-المتجهات الخطية

تُعرف المتجهات التي تقع على نفس الخط أو الخطوط المتوازية باسم المتجهات الخطية، والمعروفة أيضًا باسم المتجهات المتوازية.
4- النواقل المشتركة المستوية
تُعرف ثلاثة نواقل أو أكثر تقع في نفس المستوى أو موازية لنفس المستوى باسم النواقل المستوية.
5- النواقل المتشابهة

تُعرف المتجهات التي لها نفس الاتجاه بأنها متجهات متشابهة، على العكس من ذلك، تسمى المتجهات التي لها اتجاه متعاكس بالنسبة لبعضها البعض غير متشابهة.

ميزات المتجهات

– هناك العديد من الميزات التي تميز المتجهات وتجعلها في غاية الأهمية، حيث توفر لنا المتجهات القدرة على قياس ومعرفة الاتجاهات الموجودة في أي مبنى أو عقار مختلف، كما تساعد المتجهات على معرفة الاختلافات الموجودة بين الكميات المتجهة وبين الكميات السليمة وتمنحنا القدرة على التمييز بين هذه الكميات المختلفة.
-كما يمكننا من خلال المتجهات تصنيف الكميات الفيزيائية المختلفة إلى كميات عددية وكميات متجهة. من الممكن تمثيل ناقلات مختلفة من خلال الرسم. يتم تحليل المتجهات من خلال عدة مستويات تتضمن محورين يقعان بشكل متعامد، ومن خلالها نحصل على قيمة كل متجه ونتعرف عليه. على المكونات N وX وR