درس المتجهات في الفضاء

نتحدث عن المتجهات في الفضاء في هذه المقالة، ونذكر لك أيضًا مجموعة متنوعة من المعلومات الأخرى حول المتجهات، مثل بعض خصائص المتجهات، وخصائص المتجهات، ومكونات المتجهات.

دراسة المتجهات في الفضاء

تعريف المتجهات في الفضاء ثلاثي الأبعاد

يتم تعريف المتجه على أنه كمية لها مقدار واتجاه. هندسيًا، يمكننا أن نتخيل متجهًا على شكل قطعة مستقيمة موجهة، طولها هو مقدار المتجه، وفي نهايتها سهم يشير إلى الاتجاه. حيث يكون اتجاه المتجه من ذيله إلى رأسه. يكون المتجهان متماثلين إذا كان لهما نفس الحجم والاتجاه. هذا يعني أننا إذا أخذنا متجهًا وحركناه إلى موضع جديد مع إبقائه في الاتجاه نفسه، فإن المتجه الذي سيكون لدينا في نهاية هذه العملية هو نفس المتجه الذي كان لدينا في البداية. ومن أمثلة المتجهات نواقل القوة والسرعة؛ كل من القوة والسرعة في اتجاه محدد، بينما يشير طول المتجه إلى مقدار القوة أو السرعة.
شرح المتجهات في الرياضيات

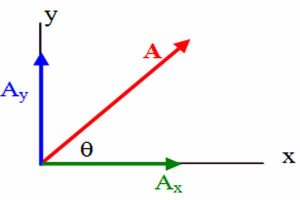
أول شيء يجب أن تتعلمه هو أن المتجه يرمز له بحرف إنجليزي ويوجد فوقه سهم هكذا ( → )، أما الكمية القياسية فيرمز لها فقط بحرف بدون سهم فوقه، وفي الصورة التالية يمكنك ملاحظة أن المتجه الذي يرمز له بالحرف (أ) هو متجه موجود في بعدين. ثانياً، وهنا سأبدأ بالشرح لكم عن المتجه ثنائي الأبعاد نظراً لسهولة هذا الموضوع. هنا، يمكن تحليل المتجه A إلى مكونين عن طريق عمل إسقاط رأسي على كل من الأفقي، ونرمز إليهما على التوالي بالرموز (AY، AX)؛ لذا يمكننا كتابة المتجه بطريقتين، الأولى بكتابة مركباته والثانية بكتابة المقدار والزاوية، ومن الشكل الهندسي السابق نستنتج أن المتجه A يمكن كتابته بالشكل التالي: (A=AY+AX) ). الطريقة الثانية هي بكتابة المقدار متبوعا بالزاوية كما يلي. : ( أ ∠θ ). لاحظ أننا أهملنا وضع السهم فوق الكميات المتجهة لصعوبة ذلك.

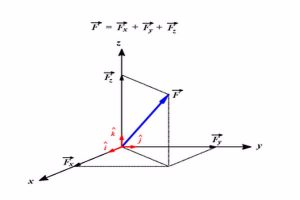
ربما لاحظتم أن الصورة أعلاه تمثل متجهًا موضوعًا في ثلاثة أبعاد، ويمكنك كتابتها بنفس الطريقة التي ذكرناها سابقًا من خلال إسقاط المتجه على المكونات الثلاثة (X، Y، Z)، بحيث يكون البعد الثالث هو البعد داخل العمق وهو (Z)، لذلك يمكنك كتابة المتجه بالطريقة التالية: (A=AX+AY+AZ) ويمكن تلخيص ما سبق كما يلي: لكتابة المتجهات في ثلاثة أبعاد، وهذا يتطلب ثلاثة محاور متعامدة بشكل متبادل. عادة، بواسطة الإحداثيات (0، 0، 0) لهذه النقطة.

بعض خواص المتجهات

1- ضرب المتجهات

المتجهات هي أيضًا كميات يمكن ضربها، حيث يمكننا ضرب متجه بكمية قياسية، وعملية ضرب متجه بكمية قياسية هي تغير في طول المتجه، أي أننا في عملية الضرب نغير مقدار المتجه، لكن اتجاهه لن يتغير إذا ضرب بأي رقم. أما بالنسبة لضرب المتجهات في بعضها البعض، هناك نوعان من ضرب المتجهات. إذا قمنا بضرب متجهين من خلال الضرب بالنقاط، فإن نتيجة هذه العملية ستكون كمية قياسية، ولذلك يعرف هذا النوع من الضرب بالضرب القياسي. والثاني من ضرب المتجهات يسمى ضرب المتجهات، وفيه تقوم بضرب المتجهين بالتقاطع بينهما، وتكون النتيجة هنا متجهًا جديدًا عموديًا على المتجهين اللذين ضربناهما.
2-المتجهات متساوية

إذا كان هناك متجهان لهما نفس الطول والمقدار، وكانا يشيران إلى نفس الاتجاه، أي يشيران إلى اتجاه واحد، ففي هذه الحالة يكون هذين المتجهين متساويين، وكمثال على تساوي المتجهات، يمكننا القول أن هناك متجهين يشيران إلى الجنوب، ومقدار كل متجه هو 5، لذلك يمكننا القول أن هذين المتجهين متساويان، ولكن إذا كان لأحد المتجهين مقدار مختلف عن الآخر أو يشير في اتجاه مختلف اتجاه من الآخر، ثم هذين المتجهات لن تكون متساوية.
3- الطرح المتجه

تقبل المتجهات أيضًا الطرح، وكما فعلنا في عملية جمع المتجهات، يمكننا العمل في الطرح، لكن لاحظ أن عملية الطرح هي نفس عملية الجمع، لكننا لن نضيف المتجهات كما فعلنا في العملية لإضافة المتجهات، ولكن في عملية الطرح سنضيف المتجه. الأول إلى سالب المتجه الثاني، أي نضيف المتجه الثاني، لكن بعد أن نعكس اتجاه هذا المتجه.
4-مجموعة المتجهات

تقبل المتجهات عملية الجمع، ويمكننا جمع المتجهات عن طريق جمع مكونات المتجه معًا. نضيف المكون السيني، والمكون y، والمكون السيني لبعضهم البعض بشكل منفصل. هناك أيضًا طريقة هندسية لإضافة المتجهات، وذلك من خلال تمثيل المتجه الأول، ثم نقوم بوضع ذيل المتجه الثاني أعلى المتجه الأول، وهكذا، في النهاية نرسم سهمًا من المتجه ذيل المتجه الأول إلى رأس المتجه الثاني، وهذا المتجه الأخير الذي رسمناه هو نتيجة عملية الجمع ويسمى المتجه الناتج، وتتميز عملية جمع المتجهات بخصائص الجمع التبادلي. والترابط.

ميزات المتجهات

1- يمكنك العمل على التمييز بين الكميات المتجهة والكميات العددية والتي تسمى الكميات العددية والكميات العددية.
2- الكمية المتجهة تصنف الكميات الفيزيائية إلى كميات عددية وكميات متجهة. ويمكن تمثيل هذه المتجهات من خلال الرسم، ويتم تحليل هذه المتجهات في العديد من المستويات التي تحتوي على محورين متعامدين، لإيجاد قيمة خاصة للمتجهات التي يتم التعرف عليها من خلال مكونات الأشعة السينية. وسادية له.
3- يتميز بتوفير إمكانية الكيانات العقارية الخاصة.
4- هذه العملية المرتبطة بالمتجهات يمكن إجراؤها في العمليات الحسابية الأساسية.
5- يساعدك هذا التطبيق على فهم الفرق بين الكميات الصحيحة والكميات المتجهة.

مكونات المتجهات

– لأي متجه هناك مكونات تعتمد على النظام الإحداثي الذي نحن فيه، وفي هذه المقالة سيتم الحديث عن نظام الإحداثيات الديكارتية. يمكن التعبير عن جميع المتجهات في المستوى الديكارتي من خلال المكونات السيني والسيني y والسيني، حيث أن أي متجه يساوي مجموع هذه المكونات الثلاثة، أي المكون السيني. مضروبًا في متجه الوحدة السيني، والمكون y مضروبًا في متجه الوحدة y، والمكون السيني مضروبًا في متجه الوحدة السيني، والمكون عبارة عن تعبير يتعلق بطول المتجه على طول محاور نظام الإحداثيات المستخدم، ويمكن القول أن طول المتجه على طول
كما ذكرنا سابقًا، يظهر متجه الوحدة عند التعبير عن المتجهات باستخدام المكونات. يمكن تعريف متجه الوحدة على أنه متجه بلا أبعاد مقداره واحد، ويعبر اتجاهه عن اتجاه كل مكون من مكونات المتجه. تختلف متجهات الوحدة حسب نظام الإحداثيات المستخدم، وإذا كان لدينا متجه في… المستويين x وy فقط، وإذا كانت الزاوية بين المحور x والمتجه هي (φ)، فإن مقدار سيكون مكون المحور x مساوياً لطول هذا المتجه مضروبًا في جيب تمام الزاوية (φ)، وسيكون طول المكون y مساويًا لطول المتجه مضروبًا في جيب الزاوية (φ) ).